1513. Прямой, центрированный и обратный порядок
Классическими
методами обхода деревьев являются:
· прямой: посещается
корень, левое поддерево, правое поддерево;
· центрированный: посещается
левое поддерево, корень, правое поддерево;
· обратный: посещается
левое поддерево, правое поддерево, корень;
Рассмотрим
рисунок:
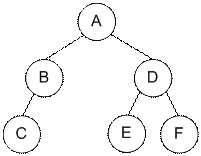
Прямой,
центрированный и обратный обходы соответственно дадут следующие
последовательности вершин: ABCDEF, CBAEDF, CBEFDA. В задаче требуется найти
последовательность вершин при обратном обходе, если известны прямой и
центрированный обходы.
Вход. Первая строка
содержит количество тестов C (C £ 2000). Каждая
следующая строка является отдельным тестом и содержит количество вершин в
бинарном дереве n (1 £ n £ 52) и две строки S1 и S2 , содержащие
соответственно прямой и центрированный обход дерева. Вершины дерева
пронумерованы разными символами из множеств a..z и A..Z. Значения n, S1 и S2 разделены пробелом.
Выход. Для каждого
теста вывести последовательность вершин при обратном обходе дерева.
|
Пример
входа |
Пример
выхода |
|
3 3 xYz Yxz 3 abc cba 6 ABCDEF
CBAEDF |
Yzx Cba CBEFDA |
РЕШЕНИЕ
рекурсия
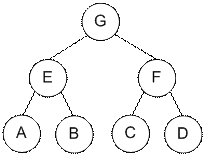
Упражнение 1. Записать порядок прямого,
центрированного и обратного обходов для следующего дерева:
Анализ алгоритма
Корень дерева
(обозначим его через A) содержится в начале последовательности прямого обхода.
Пусть последовательность прямого обхода имеет вид Ax2x3…xn,
центрированного – y1y2…ykAyk+2…yn.
В центрированном обходе ищем корень A. Тогда левое поддерево содержит вершины y1y2…yk
(всего k вершин), а правое yk+2…yn.
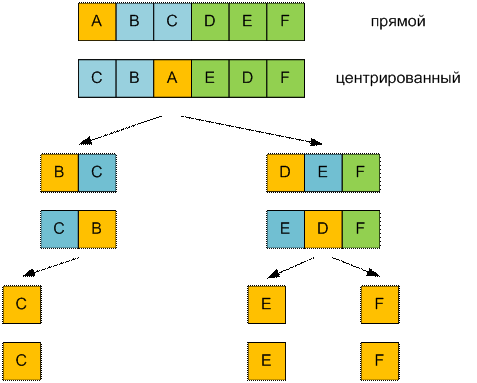
Пример
Структура дерева для третьего теста имеет
вид:
Реализация алгоритма
В символьных
массивах pre_order и in_order будем хранить последовательность вершин при
прямом и центрированном обходе дерева.
char pre_order[53],in_order[53];
Пусть
последовательность вершин при прямом обходе некоего поддерева содержится в
ячейках от pre_order[prea] до
pre_order[preb], а при центрированном
– в ячейках от in_order[ina] до
in_order[inb]. Тогда функция
post_order напечатает это поддерево в обратном порядке.
void post_order(int
ina, int inb, int
prea, int preb)
{
int
lsize,rt_in;
char root;
if (ina >
inb) return;
Корень текущего поддерева находится в
начале прямого обхода pre_order[prea].
root = pre_order[prea];
Перебором ищем позицию rt_in корня root в центрированном обходе.
for(rt_in = ina;
rt_in < inb; rt_in++)
if
(in_order[rt_in] == root) break;
В переменной lsize вычислим размер левого поддерева.
lsize = rt_in - ina;
Выводим обратный порядок: левое
поддерево, правое поддерево и корень.
post_order(ina,rt_in-1,prea+1,prea+lsize);
post_order(rt_in+1,inb,prea+1+lsize,preb);
printf("%c",root);
}
Читаем число
тестов n. Для каждого теста читаем количество вершин дерева d и
последовательность вершин при прямом и центрированном обходе дерева. Запускаем
процедуру post_order, которая и выводит искомый обратный порядок вершин.
scanf("%d",&n);
for(i = 0; i < n; i++)
{
scanf("%d %s
%s",&d,pre_order,in_order);
post_order(0,strlen(pre_order),0,strlen(in_order));
printf("\n");
}
Линейный алгоритм
Можно достигнуть
линейности по времени работы алгоритма, если за константу по времени мы сможем
находить корень в центрированном обходе. Для этого перепишем основную часть
программы, добавив препроцессинг.
scanf("%d",&tests);
for(i = 0; i < tests; i++)
{
scanf("%d %s
%s",&n,pre_order,in_order); Len = strlen(pre_order);
for (char j = 0; j < n; j++) Positions[in_order[j]] =
j;
post_order(0,0,Len);
printf("\n");
}
Равенство Positions[c] = i означает, что символ с ASCII кодом c находится в массиве in_order в ячейке с номером i.
Такой препроцессинг возможен, так как все вершины дерева имеют разные метки.
Функция post_order выводит обратный обход дерева. Ей на вход передаются
индексы начала прямого и центрированного обходов, а также количество вершин Length в текущем дереве.
void post_order(int
LeftPreOrder, int LeftInOrder, int Length)
{
if (!Length) return;
Корень дерева Root находится в центрированном обходе в позиции pos. Количество вершин в левом поддереве
newLength равно pos – LeftInOrder, в
правом Length – newLength – 1.
int Root =
pre_order[LeftPreOrder];
int pos =
Positions[Root];
int newLength
= pos - LeftInOrder;
Запускаем рекурсивный обход левого и
правого поддерева. После чего выводим значение корня Root.
post_order(LeftPreOrder+1,LeftInOrder,newLength);
post_order(LeftPreOrder+newLength+1,pos+1,Length-newLength-1);
printf("%c",Root);
}